【有道难题资格赛一】解题报告
发表时间:2010-05-31 11:11:34 浏览(4237) 评论(2)
A:另类的异或
【题目叙述】
对于普通的异或,其实是二进制的无进位的加法
这里我们定义一种另类的异或A op B, op是一个仅由^组成的字符串,如果op中包含n个^,那么A op B表示A和B之间进行n+1进制的无进位的加法。
下图展示了3 ^ 5 和 4 ^^ 5的计算过程
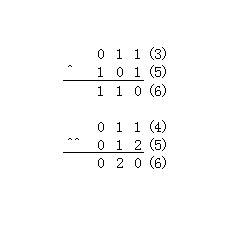
【输入】
第一行有一个正整数T, 表示下面共有T组测试数据。
接下来T行,每行有一组测试数据,是由空格隔开的三个部分组成:
A B C
A和C是两个十进制整数,B是一个字符串,由n个^组成
1 <= T <= 100, 0<=A,B<2^30, 1<=n<=1000
【输出】
每个测试数据输出一行,包含一个数字,即该数据的结果,用十进制表示。
【样例输入】
2
3 ^ 5
4 ^^ 5
【样例输出】
6
6
【算法分析】
直接纯模拟,统计每组数据中包含的"^"的个数N,将每组输入的两个数字转化成N+1进制数,然后每位做加法,加完后模(N+1),最后将结果转化回10进制数。
【我的代码】
var i,j,k,l,m,n,p,q,r,t:longint;
num1,num2,ans:array[0..100] of longint;
oup:longint;
c:char;
begin
readln(t);
for i:=1 to t do
begin
p:=0;
while true do
begin
read(c);
if (c in ['0'..'9']) then p:=p*10+ord(c)-48
else break;
end;
k:=1;
while true do
begin
read(c);
if (c='^') then break;
end;
while true do
begin
read(c);
inc(k);
if (c<>'^') then break;
end;
q:=0;
while not eoln do
begin
read(c);
if (c in ['0'..'9']) then q:=q*10+ord(c)-48;
end;
readln;
m:=0;
fillchar(num1,sizeof(num1),0);
fillchar(num2,sizeof(num2),0);
fillchar(ans,sizeof(ans),0);
while (p>0) do
begin
inc(m);
num1[m]:=p mod k;
p:=p div k;
end;
m:=0;
while (q>0) do
begin
inc(m);
num2[m]:=q mod k;
q:=q div k;
end;
for j:=1 to 100 do ans[j]:=(num1[j]+num2[j]) mod k;
for l:=100 downto 1 do if (ans[l]>0) then break;
oup:=0;
for j:=l downto 1 do oup:=oup*k+ans[j];
writeln(oup);
end;
end.
【现场总结】
诡异地RE两次,怀疑是有多个空格,于是改变了读入方式,导致读入巨长无比。
B:有道搜索框
【题目叙述】
在有道搜索框中,当输入一个或者多个字符时,搜索框会出现一定数量的提示,如下图所示:

现在给你N个单词和一些查询,请输出提示结果,为了简化这个问题,只需要输出以查询词为前缀的并且按字典序排列的最前面的8个单词,如果符合要求的单词一个也没有请只输出当前查询词。
【输入】
第一行是一个正整数N,表示词表中有N个单词。
接下来有N行,每行都有一个单词,注意词表中的单词可能有重复,请忽略掉重复单词。所有的单词都由小写字母组成。
接下来的一行有一个正整数Q,表示接下来有Q个查询。
接下来Q行,每行有一个单词,表示一个查询词,所有的查询词也都是由小写字母组成,并且所有的单词以及查询的长度都不超过20,且都不为空
其中:N<=10000,Q<=10000
【输出】
对于每个查询,输出一行,按顺序输出该查询词的提示结果,用空格隔开。
【样例输入】
10
a
ab
hello
that
those
dict
youdao
world
your
dictionary
6
bob
d
dict
dicti
yo
z
【样例输出】
bob
dict dictionary
dict dictionary
dictionary
youdao your
z
【算法分析】
用一个字母树(Trie)存储所有给定的单词。然后,每读入一个询问就试着在Trie中查找。如果在没有查找完全改询问前已经出现了空儿子,则输出该单词本身,否则,记录下Trie树中询问的末端位置,并从这个位置开始在Trie中DFS,直到按字典序输出了8个单词或者遍历整个以询问到达的末端位置为根Trie子树完毕。输出格式注意处理。
【我的代码】
var i,j,k,l,m,n,p,q,r,t,many,left:longint;
trie:array[0..200000,'a'..'z'] of longint;
have:array[0..200000] of boolean;
s:string;
can:boolean;
procedure ins_trie(s:string);
var g:longint;
begin
p:=0;
for g:=1 to length(s) do
if (trie[p,s[g]]>0) then p:=trie[p,s[g]]
else
begin
inc(many);
trie[p,s[g]]:=many;
p:=many;
end;
have[p]:=true;
end;
procedure dfs(s:string;x:longint);
var c:char;
begin
if (left=0) then exit;
if (have[x]) then
begin
if (left<8) then write(' ');
write(s);dec(left);
end;
for c:='a' to 'z' do
if trie[x,c]>0 then dfs(s+c,trie[x,c]);
end;
begin
readln(n);
many:=0;
fillchar(trie,sizeof(trie),0);
for i:=1 to n do
begin
readln(s);
ins_trie(s);
end;
readln(q);
for i:=1 to q do
begin
readln(s);
p:=0;can:=true;
for j:=1 to length(s) do
if (trie[p,s[j]]=0) then
begin
can:=false;break;
end else p:=trie[p,s[j]];
if (not can) then writeln(s) else
begin
left:=8;
dfs(s,p);writeln;
end;
end;
end.
【现场总结】
一次AC
C:最大和子序列
【题目叙述】
给一个整数数组A={a1,a2,…an}, 将这个数组首尾相接连成一个环状,它的一个子序列是指这个数组连续的一段,比如a2,a3…ak,或者an,a1…ai。请从这个环上选取两个不重叠的非空子序列,使这两个子序列中的所有数字之和最大。
在三个样例中分别选取的子序列是:
样例一: {a1} {a3}
样例二: {a1} {a3}
样例三: {a5,a1} {a3}
【输入】
输入的第一行包含一个正整数T(1<=T<=40),表示有T组测试数据。
接下来每个测试数据包含两行,第一行是一个正整数n(2<=n<=50000), 第二行是用空格隔开的数组A的n个数,依次为a1,a2,…an (|ai|<=10000)。
【输出】
每组数据输出一行,包含一个数,即所求的这两个子序列的元素之和。
【样例输入】
3
3
1 -1 0
4
1 -1 1 -1
5
1 -1 1 -1 1
【样例输出】
1
2
3
【算法分析】
这是一道动态规划问题。基于环的动态规划一般比较繁琐。从数据范围分析,对于每组数据,需要O(N)的算法。
我们把环打开,变成1..N的一个数字链。考虑我们选出的两段数,有两种情况:1、两段都不跨头尾;2、有一段跨越头尾。如下图,图中A、B表示我们选出的两段数。
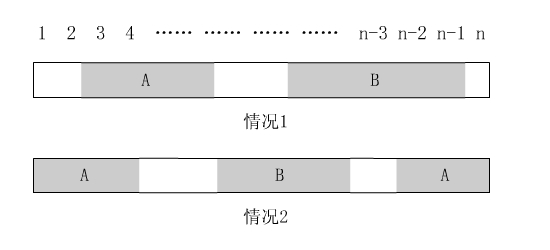
我们可以用O(N)的时间求出数串的前缀和、后缀和。i位置的前缀和left[i]表示a1+a2+...+ai,后缀和right[i]表示ai+a(i+1)+a(i+2)+...+an。同时,我们处理前缀和最大值、最小值和后缀和最大值、最小值。i位置的前缀和最大值leftmax[i]表示left[1]、left[2]...left[i]里面的最大值,i位置的后缀和最小值rightmin[i]表示right[i]、right[i+1]...right[n]里面的最小值。其他两个的含义显然了。然后,我们处理前缀最大盈利和后缀最大盈利。i位置的盈利定义为left[i]-leftmin[i-1],也就是选择了一段不包含a1的数字的最大和。那么,i位置的前缀最大盈利就是1,2...i的盈利中的最大值。后缀最大盈利的定义也显而易见了。这几个数组每个只要O(N)的时间就能求出,不明白的看程序就可以了。
为什么求这些东西呢?每个数组都是有用的。下面进入程序主体。
回到刚才说到的两种情况。情况1中的A段,可能是a1到某个位置的数字和,也可能不包括a1。如果包括a1,则是一个前缀和,否则是两个前缀和的差,即右端位置的前缀和-(左端位置-1)的前缀和。注意,缀合是面向位置的。假设我们枚举了A、B两段的分界点i,并规定A段的右端点不超过i,B段左端点必须大于i。这样就保证了两段不重叠。那么,我们这里要贪心了。对于A段包括a1,我们显然选择一个i位置的最大前缀leftmax[i];而若不包含a1,我们选择leftdt[i]。这两者中的较大值就是A段。类似的,B段应该是rightmax[i+1]和rightdt[i+1]中的较大值。
情况2麻烦一些。我们枚举B段的右端点和A段处于数列末端一半的左端点的分界点i,要求B右端点为i,末端的A段左端点不能左于i+1。那么,末端的A段比较好做,直接是rightmax[i+1]。而左边的这个就要麻烦一些。分析一下,实际上左边这部分=B的右端点位置的前缀-(B的左端点-1)的前缀+头端半段A的右端点的前缀。在循环i的时候,B的右端点位置的前缀已经确定了,那么,我们就要让-(B的左端点-1)的前缀+头端半段A的右端点的前缀最大。这个东西,我们需要再开一个数组进行预处理。我们定义i位置的最大反盈利为-left[i]+leftmax[i-1]。而i位置的最大反盈利最大值leftdt2[i]为1、2...i这些位置的最大反盈利中的最大值。这个也可以O(N)DP出来。那么,问题迎刃而解。那个比较恶心的部分的值就是left[i]+leftdt2[i-1]啦。
好了,思路就是这样。确实很繁琐,不太好理解。恕我表达能力有限,如果还不明白直接QQ问我吧。
【我的代码】
var i,j,k,l,m,n,p,q,r,s,t,dt:longint;
a:array[0..50001] of longint;
left,right,leftmax,rightmax,leftmin,rightmin,leftdt,rightdt:array[0..50001] of longint;
ans:longint;
function more(x,y:longint):longint;
begin
if (x>y) then exit(x) else exit(y);
end;
function less(x,y:longint):longint;
begin
if (x<y) then exit(x) else exit(y);
end;
begin
read(t);
for dt:=1 to t do
begin
read(n);
fillchar(left,sizeof(left),0);
fillchar(right,sizeof(right),0);
leftmax[0]:=-maxlongint;leftmin[0]:=maxlongint;
rightmax[n+1]:=-maxlongint;rightmin[n+1]:=maxlongint;
for i:=1 to n do read(a[i]);
for i:=1 to n do
begin
left[i]:=left[i-1]+a[i];
leftmax[i]:=leftmax[i-1];
if (left[i]>leftmax[i]) then leftmax[i]:=left[i];
leftmin[i]:=leftmin[i-1];
if (left[i]<leftmin[i]) then leftmin[i]:=left[i];
end;
for i:=n downto 1 do
begin
right[i]:=right[i+1]+a[i];
rightmax[i]:=rightmax[i+1];
if (right[i]>rightmax[i]) then rightmax[i]:=right[i];
rightmin[i]:=rightmin[i+1];
if (right[i]<rightmin[i]) then rightmin[i]:=right[i];
end;
ans:=-maxlongint;
for i:=1 to n-1 do
if (leftmax[i]+rightmax[i+1]>ans) then ans:=leftmax[i]+rightmax[i+1];
leftdt[1]:=left[1];
for i:=2 to n do
begin
leftdt[i]:=leftdt[i-1];
if (left[i]-leftmin[i-1]>leftdt[i]) then leftdt[i]:=left[i]-leftmin[i-1];
end;
rightdt[n]:=right[n];
for i:=n-1 downto 1 do
begin
rightdt[i]:=rightdt[i+1];
if (right[i]-rightmin[i+1]>rightdt[i]) then rightdt[i]:=right[i]-rightmin[i+1];
end;
for i:=1 to n-1 do
begin
p:=more(left[i],leftdt[i]);
q:=more(right[i+1],rightdt[i+1]);
if (p+q>ans) then ans:=p+q;
end;
leftdt[1]:=-left[1];
for i:=2 to n do
leftdt[i]:=more(leftdt[i-1],-left[i]+leftmax[i-1]);
for i:=2 to n-1 do
ans:=more(ans,left[i]+leftdt[i-1]+rightmax[i+1]);
writeln(ans);
end;
end.
【现场总结】
一次AC
【整场比赛总揽】
分数:1000
罚时:03:19:25
排名:122
【题目叙述】
对于普通的异或,其实是二进制的无进位的加法
这里我们定义一种另类的异或A op B, op是一个仅由^组成的字符串,如果op中包含n个^,那么A op B表示A和B之间进行n+1进制的无进位的加法。
下图展示了3 ^ 5 和 4 ^^ 5的计算过程
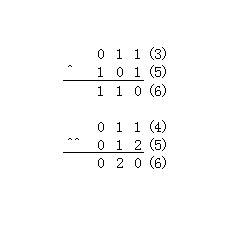
【输入】
第一行有一个正整数T, 表示下面共有T组测试数据。
接下来T行,每行有一组测试数据,是由空格隔开的三个部分组成:
A B C
A和C是两个十进制整数,B是一个字符串,由n个^组成
1 <= T <= 100, 0<=A,B<2^30, 1<=n<=1000
【输出】
每个测试数据输出一行,包含一个数字,即该数据的结果,用十进制表示。
【样例输入】
2
3 ^ 5
4 ^^ 5
【样例输出】
6
6
【算法分析】
直接纯模拟,统计每组数据中包含的"^"的个数N,将每组输入的两个数字转化成N+1进制数,然后每位做加法,加完后模(N+1),最后将结果转化回10进制数。
【我的代码】
var i,j,k,l,m,n,p,q,r,t:longint;
num1,num2,ans:array[0..100] of longint;
oup:longint;
c:char;
begin
readln(t);
for i:=1 to t do
begin
p:=0;
while true do
begin
read(c);
if (c in ['0'..'9']) then p:=p*10+ord(c)-48
else break;
end;
k:=1;
while true do
begin
read(c);
if (c='^') then break;
end;
while true do
begin
read(c);
inc(k);
if (c<>'^') then break;
end;
q:=0;
while not eoln do
begin
read(c);
if (c in ['0'..'9']) then q:=q*10+ord(c)-48;
end;
readln;
m:=0;
fillchar(num1,sizeof(num1),0);
fillchar(num2,sizeof(num2),0);
fillchar(ans,sizeof(ans),0);
while (p>0) do
begin
inc(m);
num1[m]:=p mod k;
p:=p div k;
end;
m:=0;
while (q>0) do
begin
inc(m);
num2[m]:=q mod k;
q:=q div k;
end;
for j:=1 to 100 do ans[j]:=(num1[j]+num2[j]) mod k;
for l:=100 downto 1 do if (ans[l]>0) then break;
oup:=0;
for j:=l downto 1 do oup:=oup*k+ans[j];
writeln(oup);
end;
end.
【现场总结】
诡异地RE两次,怀疑是有多个空格,于是改变了读入方式,导致读入巨长无比。
B:有道搜索框
【题目叙述】
在有道搜索框中,当输入一个或者多个字符时,搜索框会出现一定数量的提示,如下图所示:

现在给你N个单词和一些查询,请输出提示结果,为了简化这个问题,只需要输出以查询词为前缀的并且按字典序排列的最前面的8个单词,如果符合要求的单词一个也没有请只输出当前查询词。
【输入】
第一行是一个正整数N,表示词表中有N个单词。
接下来有N行,每行都有一个单词,注意词表中的单词可能有重复,请忽略掉重复单词。所有的单词都由小写字母组成。
接下来的一行有一个正整数Q,表示接下来有Q个查询。
接下来Q行,每行有一个单词,表示一个查询词,所有的查询词也都是由小写字母组成,并且所有的单词以及查询的长度都不超过20,且都不为空
其中:N<=10000,Q<=10000
【输出】
对于每个查询,输出一行,按顺序输出该查询词的提示结果,用空格隔开。
【样例输入】
10
a
ab
hello
that
those
dict
youdao
world
your
dictionary
6
bob
d
dict
dicti
yo
z
【样例输出】
bob
dict dictionary
dict dictionary
dictionary
youdao your
z
【算法分析】
用一个字母树(Trie)存储所有给定的单词。然后,每读入一个询问就试着在Trie中查找。如果在没有查找完全改询问前已经出现了空儿子,则输出该单词本身,否则,记录下Trie树中询问的末端位置,并从这个位置开始在Trie中DFS,直到按字典序输出了8个单词或者遍历整个以询问到达的末端位置为根Trie子树完毕。输出格式注意处理。
【我的代码】
var i,j,k,l,m,n,p,q,r,t,many,left:longint;
trie:array[0..200000,'a'..'z'] of longint;
have:array[0..200000] of boolean;
s:string;
can:boolean;
procedure ins_trie(s:string);
var g:longint;
begin
p:=0;
for g:=1 to length(s) do
if (trie[p,s[g]]>0) then p:=trie[p,s[g]]
else
begin
inc(many);
trie[p,s[g]]:=many;
p:=many;
end;
have[p]:=true;
end;
procedure dfs(s:string;x:longint);
var c:char;
begin
if (left=0) then exit;
if (have[x]) then
begin
if (left<8) then write(' ');
write(s);dec(left);
end;
for c:='a' to 'z' do
if trie[x,c]>0 then dfs(s+c,trie[x,c]);
end;
begin
readln(n);
many:=0;
fillchar(trie,sizeof(trie),0);
for i:=1 to n do
begin
readln(s);
ins_trie(s);
end;
readln(q);
for i:=1 to q do
begin
readln(s);
p:=0;can:=true;
for j:=1 to length(s) do
if (trie[p,s[j]]=0) then
begin
can:=false;break;
end else p:=trie[p,s[j]];
if (not can) then writeln(s) else
begin
left:=8;
dfs(s,p);writeln;
end;
end;
end.
【现场总结】
一次AC
C:最大和子序列
【题目叙述】
给一个整数数组A={a1,a2,…an}, 将这个数组首尾相接连成一个环状,它的一个子序列是指这个数组连续的一段,比如a2,a3…ak,或者an,a1…ai。请从这个环上选取两个不重叠的非空子序列,使这两个子序列中的所有数字之和最大。
在三个样例中分别选取的子序列是:
样例一: {a1} {a3}
样例二: {a1} {a3}
样例三: {a5,a1} {a3}
【输入】
输入的第一行包含一个正整数T(1<=T<=40),表示有T组测试数据。
接下来每个测试数据包含两行,第一行是一个正整数n(2<=n<=50000), 第二行是用空格隔开的数组A的n个数,依次为a1,a2,…an (|ai|<=10000)。
【输出】
每组数据输出一行,包含一个数,即所求的这两个子序列的元素之和。
【样例输入】
3
3
1 -1 0
4
1 -1 1 -1
5
1 -1 1 -1 1
【样例输出】
1
2
3
【算法分析】
这是一道动态规划问题。基于环的动态规划一般比较繁琐。从数据范围分析,对于每组数据,需要O(N)的算法。
我们把环打开,变成1..N的一个数字链。考虑我们选出的两段数,有两种情况:1、两段都不跨头尾;2、有一段跨越头尾。如下图,图中A、B表示我们选出的两段数。

我们可以用O(N)的时间求出数串的前缀和、后缀和。i位置的前缀和left[i]表示a1+a2+...+ai,后缀和right[i]表示ai+a(i+1)+a(i+2)+...+an。同时,我们处理前缀和最大值、最小值和后缀和最大值、最小值。i位置的前缀和最大值leftmax[i]表示left[1]、left[2]...left[i]里面的最大值,i位置的后缀和最小值rightmin[i]表示right[i]、right[i+1]...right[n]里面的最小值。其他两个的含义显然了。然后,我们处理前缀最大盈利和后缀最大盈利。i位置的盈利定义为left[i]-leftmin[i-1],也就是选择了一段不包含a1的数字的最大和。那么,i位置的前缀最大盈利就是1,2...i的盈利中的最大值。后缀最大盈利的定义也显而易见了。这几个数组每个只要O(N)的时间就能求出,不明白的看程序就可以了。
为什么求这些东西呢?每个数组都是有用的。下面进入程序主体。
回到刚才说到的两种情况。情况1中的A段,可能是a1到某个位置的数字和,也可能不包括a1。如果包括a1,则是一个前缀和,否则是两个前缀和的差,即右端位置的前缀和-(左端位置-1)的前缀和。注意,缀合是面向位置的。假设我们枚举了A、B两段的分界点i,并规定A段的右端点不超过i,B段左端点必须大于i。这样就保证了两段不重叠。那么,我们这里要贪心了。对于A段包括a1,我们显然选择一个i位置的最大前缀leftmax[i];而若不包含a1,我们选择leftdt[i]。这两者中的较大值就是A段。类似的,B段应该是rightmax[i+1]和rightdt[i+1]中的较大值。
情况2麻烦一些。我们枚举B段的右端点和A段处于数列末端一半的左端点的分界点i,要求B右端点为i,末端的A段左端点不能左于i+1。那么,末端的A段比较好做,直接是rightmax[i+1]。而左边的这个就要麻烦一些。分析一下,实际上左边这部分=B的右端点位置的前缀-(B的左端点-1)的前缀+头端半段A的右端点的前缀。在循环i的时候,B的右端点位置的前缀已经确定了,那么,我们就要让-(B的左端点-1)的前缀+头端半段A的右端点的前缀最大。这个东西,我们需要再开一个数组进行预处理。我们定义i位置的最大反盈利为-left[i]+leftmax[i-1]。而i位置的最大反盈利最大值leftdt2[i]为1、2...i这些位置的最大反盈利中的最大值。这个也可以O(N)DP出来。那么,问题迎刃而解。那个比较恶心的部分的值就是left[i]+leftdt2[i-1]啦。
好了,思路就是这样。确实很繁琐,不太好理解。恕我表达能力有限,如果还不明白直接QQ问我吧。
【我的代码】
var i,j,k,l,m,n,p,q,r,s,t,dt:longint;
a:array[0..50001] of longint;
left,right,leftmax,rightmax,leftmin,rightmin,leftdt,rightdt:array[0..50001] of longint;
ans:longint;
function more(x,y:longint):longint;
begin
if (x>y) then exit(x) else exit(y);
end;
function less(x,y:longint):longint;
begin
if (x<y) then exit(x) else exit(y);
end;
begin
read(t);
for dt:=1 to t do
begin
read(n);
fillchar(left,sizeof(left),0);
fillchar(right,sizeof(right),0);
leftmax[0]:=-maxlongint;leftmin[0]:=maxlongint;
rightmax[n+1]:=-maxlongint;rightmin[n+1]:=maxlongint;
for i:=1 to n do read(a[i]);
for i:=1 to n do
begin
left[i]:=left[i-1]+a[i];
leftmax[i]:=leftmax[i-1];
if (left[i]>leftmax[i]) then leftmax[i]:=left[i];
leftmin[i]:=leftmin[i-1];
if (left[i]<leftmin[i]) then leftmin[i]:=left[i];
end;
for i:=n downto 1 do
begin
right[i]:=right[i+1]+a[i];
rightmax[i]:=rightmax[i+1];
if (right[i]>rightmax[i]) then rightmax[i]:=right[i];
rightmin[i]:=rightmin[i+1];
if (right[i]<rightmin[i]) then rightmin[i]:=right[i];
end;
ans:=-maxlongint;
for i:=1 to n-1 do
if (leftmax[i]+rightmax[i+1]>ans) then ans:=leftmax[i]+rightmax[i+1];
leftdt[1]:=left[1];
for i:=2 to n do
begin
leftdt[i]:=leftdt[i-1];
if (left[i]-leftmin[i-1]>leftdt[i]) then leftdt[i]:=left[i]-leftmin[i-1];
end;
rightdt[n]:=right[n];
for i:=n-1 downto 1 do
begin
rightdt[i]:=rightdt[i+1];
if (right[i]-rightmin[i+1]>rightdt[i]) then rightdt[i]:=right[i]-rightmin[i+1];
end;
for i:=1 to n-1 do
begin
p:=more(left[i],leftdt[i]);
q:=more(right[i+1],rightdt[i+1]);
if (p+q>ans) then ans:=p+q;
end;
leftdt[1]:=-left[1];
for i:=2 to n do
leftdt[i]:=more(leftdt[i-1],-left[i]+leftmax[i-1]);
for i:=2 to n-1 do
ans:=more(ans,left[i]+leftdt[i-1]+rightmax[i+1]);
writeln(ans);
end;
end.
【现场总结】
一次AC
【整场比赛总揽】
分数:1000
罚时:03:19:25
排名:122
网友评论:
| 1 Guest 于 2010-06-03 23:51:33 说: | 回复 | |
|---|---|---|
第三题有难度 | ||
| 2 Admin 于 2010-06-05 19:00:31 说: | 回复 | |
回复Guest:暂时不支持留言超链接功能。 |



