【有道难题资格赛三】解题报告
发表时间:2010-05-31 13:29:52 浏览(8611) 评论(3)
A:选课的困惑
【题目叙述】
小明打算本科毕业后申请出国,不过他想申请一个好学校,所有课程的加权平均分必须达到90分及以上。
现在小明已经修完所有的必修课,他想通过修一些选修课让课程加权平均分最终达到他的要求。一共有m门选修课可以随意选修,且他能很明确知道选修每个选修课能得到的分数,请问至少修多少门课才能达到他的要求?假设共有k门课程,其总的加权平均分的计算方法如下:
加权平均分=(成绩1*学分1+成绩2*学分2+……成绩k*学分k) / (学分1+学分2+……学分k)
【输入】
第一行包含一个正整数T,表示有T组测试数据。
每个测试数据第一行包含空格隔开的两个正整数n和m,表示小明已修完了n门必修课,还有m门选修课可供选择。
接下来有n行,每行包含空格隔开的一个实数ai和一个整数bi,分别表示小明第i门课的成绩以及第i门课的学分数
接下来有m行,每行包含空格隔开的一个实数cj和一个整数dj,分别表示小明第j门选修课可以获得的预期分数以及第j门选修课的学分数。
其中:
1<=T<=100, 1 <= n,m <= 100, 0 <= ai, cj <= 100, 1 <= bi, dj <= 5,所有的分数小数点后至多两位。
【输出】
每组测试数据输出一行,如果可以达到要求,则输出一个整数k,表示小明至少要修的选修课数目,如果小明修完所有的选修课都不可能达到要求,则输出 Impossible
【样例输入】
2
3 4
80.00 1
40.00 2
20.00 2
90.00 3
88.00 2
92.00 2
100.00 1
3 4
62.00 1
70.00 1
80.00 1
99.00 2
100.00 2
100.00 2
100.00 2
【样例输出】
Impossible
3
【算法分析】
贪心。实际是需要满足不等式(成绩1*学分1+成绩2*学分2+……成绩k*学分k) / (学分1+学分2+……学分k)>=90。我们把分母乘到不等号等号右边:成绩1*学分1+成绩2*学分2+……成绩k*学分k>=90*(学分1+学分2+……学分k)。现在不满足这个式子,右边-左边=我们需要弥补的部分。好的,我们有一门选修课,小明的得分是ai,学分是bi。如果选了这门课,不等式等号左边加上ai*bi,右边要加上90*bi。可以弥补(ai-90)*bi这么多的分差。好的,我们就以m门课的 (ai-90)*bi作为依据从大到小排序,然后依次选课,直到弥补成功跳出。所选课的数量就是答案。如果选所有课依然不能弥补,输出Impossible。
【我的代码】
var i,j,k,l,m,n,p,q,r,s,t,d:longint;
cg:array[0..1000] of double;
dt,mid,mm:double;
ans:longint;
begin
read(t);
for d:=1 to t do
begin
read(n,m);
dt:=0;
for i:=1 to n do
begin
read(mid,k);
dt:=dt+(mid-90)*k;
end;
for i:=1 to m do
begin
read(mid,k);
cg[i]:=(mid-90)*k;
end;
if (dt>=0) then
begin
writeln(0);
continue;
end;
for i:=1 to m-1 do
for j:=i+1 to m do
if (cg[i]<cg[j]) then
begin
mm:=cg[i];cg[i]:=cg[j];cg[j]:=mm;
end;
for i:=1 to m do
begin
dt:=dt+cg[i];
if (dt>=0) then break;
end;
if (dt>=0) then writeln(i) else writeln('Impossible');
end;
end.
【现场分析】
一次AC
B:X星球的身份证系统
【题目叙述】
在X星球上的外星人和地球上一样拥有一个长N位的身份证号码,而X星球的人使用的是一种26进制身份证号码,用a~z表示。
在X星球上正在举行一次幸运者抽奖活动,X星球的政府首脑制定了一个特殊的抽奖规则,凡是身份证号码符合对称性质(回文串)的人就能够成为本次活动的幸运者。
现在你知道X星球中最大的身份证号码,希望你能够计算出最多有多少人将成为本次活动的幸运者。
【输入】
输入数据的第一行为一个正整数N,第二行为一个长度为N的字符串,表示已知的最大身份证号码.
其中 N <= 30
【输出】
本次活动的最大幸运人数模10000的结果.
【样例输入】
3
bca
【样例输出】
28
【算法分析】
数学题。枚举前一半,后一半的对应位置的数字相同。当比给定位小的时候,中间部分任意回文;当相等时,则枚举下一位。要考虑很多特殊情形,当原数字中后面出现了某一位比右侧对应位置的数字大时,则最中间的一位不能达到原数字;当又出现了一位小于时,则中间数字又可以相等。我是用can这个boolean变量记录的。
【我的代码】
var i,j,k,l,m,n,p,q,r,t,ans:longint;
c:array[0..30] of longint;
esl:array[0..30] of longint;
ch:char;
can:boolean;
function hw(x:longint):longint;
begin
exit(esl[x div 2+x mod 2]);
end;
begin
readln(n);
for i:=1 to n do
begin
read(ch);
c[i]:=ord(ch)-ord('a')+1;
end;
if (n=1) then
begin
writeln(c[1]);
halt;
end;
esl[0]:=1;
for i:=1 to 30 do esl[i]:=(esl[i-1]*26) mod 10000;
k:=n div 2;
ans:=0;can:=true;
for i:=1 to k do
begin
ans:=(ans+hw(n-i*2)*(c[i]-1)) mod 10000;
if (c[i]>c[n-i+1]) then can:=false;
if (c[i]<c[n-i+1]) then can:=true;
end;
if (n mod 2=0) then
begin
if (c[k]<=c[k+1]) then if can then ans:=(ans+1) mod 10000;
end else
begin
if (can) then
ans:=(ans+c[k+1]) mod 10000 else
ans:=(ans+c[k+1]-1) mod 10000;
end;
writeln(ans);
end.
【现场分析】
没记录can以及忘记了中间部分也要回文,WA了两次
C:火柴游戏
【题目叙述】
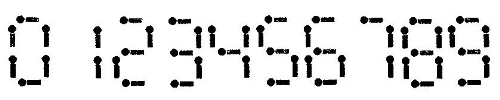
如上图所示,我们可以用不同数量的火柴排成0~9这10个数字。现在这个问题需要让聪明的你来计算一下,给你N根火柴,总共可以组合成多少个被M取余后结果是素数的数字。
注意,N根火柴都要用上,另外,除了0,其他数字均不能出现前导零。
【输入】
第一行有一个正整数T,表示有T组测试数据。
接下来T行每一行表示一组测试数据,每行包含空格隔开的两个正整数N和M。
其中:
T < =20,
N, M <=10000并且M*N<=1000000
【输出】
对于每一个测试数据,请输出一行,包含一个数,即结果对1000000007取模的值。
【样例输入】
4
4 15
20 4
6 10
6 20
【样例输出】
1
6982
1
2
【算法分析】
DP。dp[i,j]表示用了i个火柴,得到的数字模m等于j的情况总数。us[k](k=0..9)表示摆k用的火柴数量。则我们把每个dp[i,j]加到dp[i+us[k],(j*10+k) mod m]上面。最终我们对dp[n,p](p为小于m的质数)求和就是答案。复杂度O(T*N*M*10)
【我的代码】
const us:array[0..9] of longint=(6,2,5,5,4,5,6,3,7,6);
mo=1000000007;
var i,j,k,l,m,n,p,q,r,s,t,d,pp:longint;
dp:array[0..2000000] of longint;
prime:array[1..10000] of longint;
pre:array[0..10000,0..9] of longint;
oup:longint;
function pr(x:longint):boolean;
var g:longint;
begin
if (x<2) then exit(false);
if (x=2) then exit(true);
for g:=2 to trunc(sqrt(x)) do
if (x mod g=0) then exit(false);
exit(true);
end;
begin
pp:=0;
for i:=2 to 10000 do if (pr(i)) then
begin
inc(pp);prime[pp]:=i;
end;
read(t);
for d:=1 to t do
begin
read(n,m);
fillchar(dp,sizeof(dp),0);
for i:=1 to 9 do inc(dp[us[i]*m+i mod m]);
for i:=0 to m-1 do
for j:=0 to 9 do
pre[i,j]:=(i*10+j) mod m;
for i:=2 to n-2 do
for j:=0 to m-1 do
begin
p:=i*m+j;
if (dp[p]=0) then continue;
for k:=0 to 9 do
begin
q:=(i+us[k])*m+pre[j,k];
dp[q]:=(dp[q]+dp[p]) mod mo;
end;
end;
oup:=0;
for i:=1 to pp do
begin
if (prime[i]>=m) then break;
oup:=(oup+dp[n*m+prime[i]]) mod mo;
end;
writeln(oup);
end;
end.
【现场总结】
这道题没过,TLE!常数优化不够!悲剧!
【整场比赛总揽】
得分:500
罚时:01:46:56
排名:271
结果:晋级
【题目叙述】
小明打算本科毕业后申请出国,不过他想申请一个好学校,所有课程的加权平均分必须达到90分及以上。
现在小明已经修完所有的必修课,他想通过修一些选修课让课程加权平均分最终达到他的要求。一共有m门选修课可以随意选修,且他能很明确知道选修每个选修课能得到的分数,请问至少修多少门课才能达到他的要求?假设共有k门课程,其总的加权平均分的计算方法如下:
加权平均分=(成绩1*学分1+成绩2*学分2+……成绩k*学分k) / (学分1+学分2+……学分k)
【输入】
第一行包含一个正整数T,表示有T组测试数据。
每个测试数据第一行包含空格隔开的两个正整数n和m,表示小明已修完了n门必修课,还有m门选修课可供选择。
接下来有n行,每行包含空格隔开的一个实数ai和一个整数bi,分别表示小明第i门课的成绩以及第i门课的学分数
接下来有m行,每行包含空格隔开的一个实数cj和一个整数dj,分别表示小明第j门选修课可以获得的预期分数以及第j门选修课的学分数。
其中:
1<=T<=100, 1 <= n,m <= 100, 0 <= ai, cj <= 100, 1 <= bi, dj <= 5,所有的分数小数点后至多两位。
【输出】
每组测试数据输出一行,如果可以达到要求,则输出一个整数k,表示小明至少要修的选修课数目,如果小明修完所有的选修课都不可能达到要求,则输出 Impossible
【样例输入】
2
3 4
80.00 1
40.00 2
20.00 2
90.00 3
88.00 2
92.00 2
100.00 1
3 4
62.00 1
70.00 1
80.00 1
99.00 2
100.00 2
100.00 2
100.00 2
【样例输出】
Impossible
3
【算法分析】
贪心。实际是需要满足不等式(成绩1*学分1+成绩2*学分2+……成绩k*学分k) / (学分1+学分2+……学分k)>=90。我们把分母乘到不等号等号右边:成绩1*学分1+成绩2*学分2+……成绩k*学分k>=90*(学分1+学分2+……学分k)。现在不满足这个式子,右边-左边=我们需要弥补的部分。好的,我们有一门选修课,小明的得分是ai,学分是bi。如果选了这门课,不等式等号左边加上ai*bi,右边要加上90*bi。可以弥补(ai-90)*bi这么多的分差。好的,我们就以m门课的 (ai-90)*bi作为依据从大到小排序,然后依次选课,直到弥补成功跳出。所选课的数量就是答案。如果选所有课依然不能弥补,输出Impossible。
【我的代码】
var i,j,k,l,m,n,p,q,r,s,t,d:longint;
cg:array[0..1000] of double;
dt,mid,mm:double;
ans:longint;
begin
read(t);
for d:=1 to t do
begin
read(n,m);
dt:=0;
for i:=1 to n do
begin
read(mid,k);
dt:=dt+(mid-90)*k;
end;
for i:=1 to m do
begin
read(mid,k);
cg[i]:=(mid-90)*k;
end;
if (dt>=0) then
begin
writeln(0);
continue;
end;
for i:=1 to m-1 do
for j:=i+1 to m do
if (cg[i]<cg[j]) then
begin
mm:=cg[i];cg[i]:=cg[j];cg[j]:=mm;
end;
for i:=1 to m do
begin
dt:=dt+cg[i];
if (dt>=0) then break;
end;
if (dt>=0) then writeln(i) else writeln('Impossible');
end;
end.
【现场分析】
一次AC
B:X星球的身份证系统
【题目叙述】
在X星球上的外星人和地球上一样拥有一个长N位的身份证号码,而X星球的人使用的是一种26进制身份证号码,用a~z表示。
在X星球上正在举行一次幸运者抽奖活动,X星球的政府首脑制定了一个特殊的抽奖规则,凡是身份证号码符合对称性质(回文串)的人就能够成为本次活动的幸运者。
现在你知道X星球中最大的身份证号码,希望你能够计算出最多有多少人将成为本次活动的幸运者。
【输入】
输入数据的第一行为一个正整数N,第二行为一个长度为N的字符串,表示已知的最大身份证号码.
其中 N <= 30
【输出】
本次活动的最大幸运人数模10000的结果.
【样例输入】
3
bca
【样例输出】
28
【算法分析】
数学题。枚举前一半,后一半的对应位置的数字相同。当比给定位小的时候,中间部分任意回文;当相等时,则枚举下一位。要考虑很多特殊情形,当原数字中后面出现了某一位比右侧对应位置的数字大时,则最中间的一位不能达到原数字;当又出现了一位小于时,则中间数字又可以相等。我是用can这个boolean变量记录的。
【我的代码】
var i,j,k,l,m,n,p,q,r,t,ans:longint;
c:array[0..30] of longint;
esl:array[0..30] of longint;
ch:char;
can:boolean;
function hw(x:longint):longint;
begin
exit(esl[x div 2+x mod 2]);
end;
begin
readln(n);
for i:=1 to n do
begin
read(ch);
c[i]:=ord(ch)-ord('a')+1;
end;
if (n=1) then
begin
writeln(c[1]);
halt;
end;
esl[0]:=1;
for i:=1 to 30 do esl[i]:=(esl[i-1]*26) mod 10000;
k:=n div 2;
ans:=0;can:=true;
for i:=1 to k do
begin
ans:=(ans+hw(n-i*2)*(c[i]-1)) mod 10000;
if (c[i]>c[n-i+1]) then can:=false;
if (c[i]<c[n-i+1]) then can:=true;
end;
if (n mod 2=0) then
begin
if (c[k]<=c[k+1]) then if can then ans:=(ans+1) mod 10000;
end else
begin
if (can) then
ans:=(ans+c[k+1]) mod 10000 else
ans:=(ans+c[k+1]-1) mod 10000;
end;
writeln(ans);
end.
【现场分析】
没记录can以及忘记了中间部分也要回文,WA了两次
C:火柴游戏
【题目叙述】
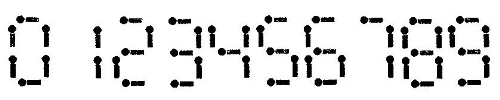
如上图所示,我们可以用不同数量的火柴排成0~9这10个数字。现在这个问题需要让聪明的你来计算一下,给你N根火柴,总共可以组合成多少个被M取余后结果是素数的数字。
注意,N根火柴都要用上,另外,除了0,其他数字均不能出现前导零。
【输入】
第一行有一个正整数T,表示有T组测试数据。
接下来T行每一行表示一组测试数据,每行包含空格隔开的两个正整数N和M。
其中:
T < =20,
N, M <=10000并且M*N<=1000000
【输出】
对于每一个测试数据,请输出一行,包含一个数,即结果对1000000007取模的值。
【样例输入】
4
4 15
20 4
6 10
6 20
【样例输出】
1
6982
1
2
【算法分析】
DP。dp[i,j]表示用了i个火柴,得到的数字模m等于j的情况总数。us[k](k=0..9)表示摆k用的火柴数量。则我们把每个dp[i,j]加到dp[i+us[k],(j*10+k) mod m]上面。最终我们对dp[n,p](p为小于m的质数)求和就是答案。复杂度O(T*N*M*10)
【我的代码】
const us:array[0..9] of longint=(6,2,5,5,4,5,6,3,7,6);
mo=1000000007;
var i,j,k,l,m,n,p,q,r,s,t,d,pp:longint;
dp:array[0..2000000] of longint;
prime:array[1..10000] of longint;
pre:array[0..10000,0..9] of longint;
oup:longint;
function pr(x:longint):boolean;
var g:longint;
begin
if (x<2) then exit(false);
if (x=2) then exit(true);
for g:=2 to trunc(sqrt(x)) do
if (x mod g=0) then exit(false);
exit(true);
end;
begin
pp:=0;
for i:=2 to 10000 do if (pr(i)) then
begin
inc(pp);prime[pp]:=i;
end;
read(t);
for d:=1 to t do
begin
read(n,m);
fillchar(dp,sizeof(dp),0);
for i:=1 to 9 do inc(dp[us[i]*m+i mod m]);
for i:=0 to m-1 do
for j:=0 to 9 do
pre[i,j]:=(i*10+j) mod m;
for i:=2 to n-2 do
for j:=0 to m-1 do
begin
p:=i*m+j;
if (dp[p]=0) then continue;
for k:=0 to 9 do
begin
q:=(i+us[k])*m+pre[j,k];
dp[q]:=(dp[q]+dp[p]) mod mo;
end;
end;
oup:=0;
for i:=1 to pp do
begin
if (prime[i]>=m) then break;
oup:=(oup+dp[n*m+prime[i]]) mod mo;
end;
writeln(oup);
end;
end.
【现场总结】
这道题没过,TLE!常数优化不够!悲剧!
【整场比赛总揽】
得分:500
罚时:01:46:56
排名:271
结果:晋级
网友评论:
| 1 Guest 于 2010-06-02 15:53:03 说: | 回复 | |
|---|---|---|
貌似那个C用Pascal写很有劣势。。相同的做法我用C++卡过去了的。。 | ||
| 2 Admin 于 2010-06-02 21:08:08 说: | 回复 | |
回复Guest:同感!膜拜Pascal过此题的牛人们!话说您是用两种语言做的比赛?比赛中同一个选手不同的题能使用不同的语言提交? | ||
| 3 leijiankun 于 2011-05-22 11:27:21 说: | 回复 | |
膜拜神牛。
我用c++写了第一个。ok的。 |



